极客算法

OpenGL1.8 - 相机Camera

2023-01-12
Graphics
 

OpenGL本身没有Camera定义，但是可以通过移动世界，给一个我们自己在动的错觉

观察空间

观察空间(View Space)也叫Camera Space或者Eye Space, 需要把世界空间转换成观察空间，也就是从相机的视角，观察世界空间的样子。

定义相机，我们需要它在世界空间中的位置、观察的方向、一个指向它右侧的向量以及一个指向它上方的向量。也就是以相机位置为原点的一个坐标系。

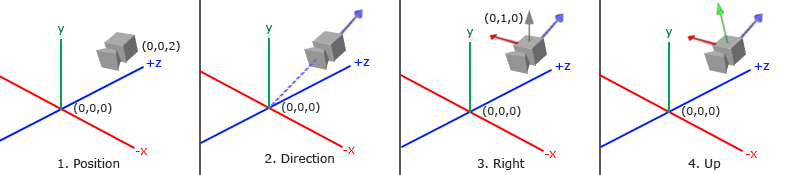
相机坐标系

相机位置

如图，在世界空间定义相机的位置如下:

glm::vec3 cameraPos = glm::vec3(0.0f, 0.0f, 2.0f);

相机方向Z

尽管相机指向z的负方向，但是作为View Space我们希望坐标轴指向为正

让相机指向世界空间原点，根据向量相减的几何意义，得到一新的向量，新的向量由target坐标指向pos坐标，也就是我们想要的z的方向。

glm::vec3 cameraTarget = glm::vec3(0.0f, 0.0f, 0.0f);
glm::vec3 cameraDirection = glm::normalize(cameraPos - cameraTarget);

相机右轴X

首先在世界空间定义个向上的单位向量， 然后将该向量与相机方向做叉乘, 会得到一个垂直于单位向量和相机方向的新向量，根据右手定则，新的向量即是我们想要的View Space的x轴

glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f); 
glm::vec3 cameraRight = glm::normalize(glm::cross(up, cameraDirection));

有了x轴和z轴, 那么z轴于x轴，就是我们想要的y轴

相机上轴Y

glm::vec3 cameraUp = glm::cross(cameraDirection, cameraRight);

注视目标

矩阵的好处是，如果有3个两两垂直(或非线性)的轴定义一个坐标空间，可以用这三个轴外加一个平移向量来创建一个矩阵。并且用这个矩阵乘以任何向量，将其转换空间。

$ LookAt = \begin{bmatrix} \color{red}{R_x} & \color{red}{R_y} & \color{red}{R_z} & 0 \\ \color{green}{U_x} & \color{green}{U_y} & \color{green}{U_z} & 0 \\ \color{blue}{D_x} & \color{blue}{D_y} & \color{blue}{D_z} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & -\color{purple}{P_x} \\ 0 & 1 & 0 & -\color{purple}{P_y} \\ 0 & 0 & 1 & -\color{purple}{P_z} \\ 0 & 0 & 0 & 1 \end{bmatrix} $

R为相机右轴，U为相机上轴, D为相机方向， P位相机位置。

注意，左边是旋转矩阵，右边是平移矩阵

GLM已经做了这项任务，我们只需要传入相机坐标P， Target坐标, 世界空间的向上坐标

glm::mat4 view;
view = glm::lookAt(glm::vec3(0.0f, 0.0f, 2.0f), 
                   glm::vec3(0.0f, 0.0f, 0.0f), 
                   glm::vec3(0.0f, 1.0f, 0.0f));

定点环绕

三角学

用三角学创建一个圆圈，让相机的位置圆圈上旋转，始终看向世界空间的原点

const float radius = 10.0f;
float camX = sin(glfwGetTime()) * radius;
float camZ = cos(glfwGetTime()) * radius;
glm::mat4 view;
view = glm::lookAt(glm::vec3(camX, 0.0, camZ), glm::vec3(0.0, 0.0, 0.0), glm::vec3(0.0, 1.0, 0.0));

结果

源码

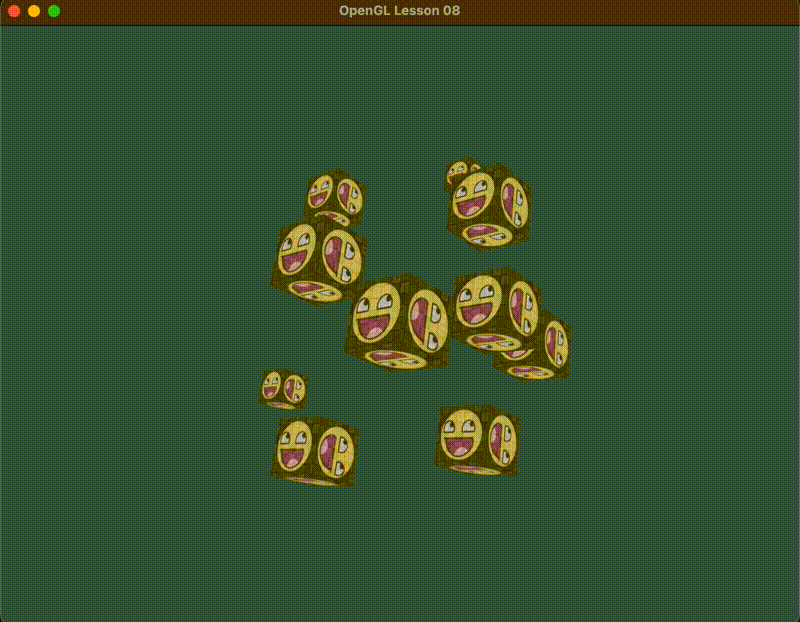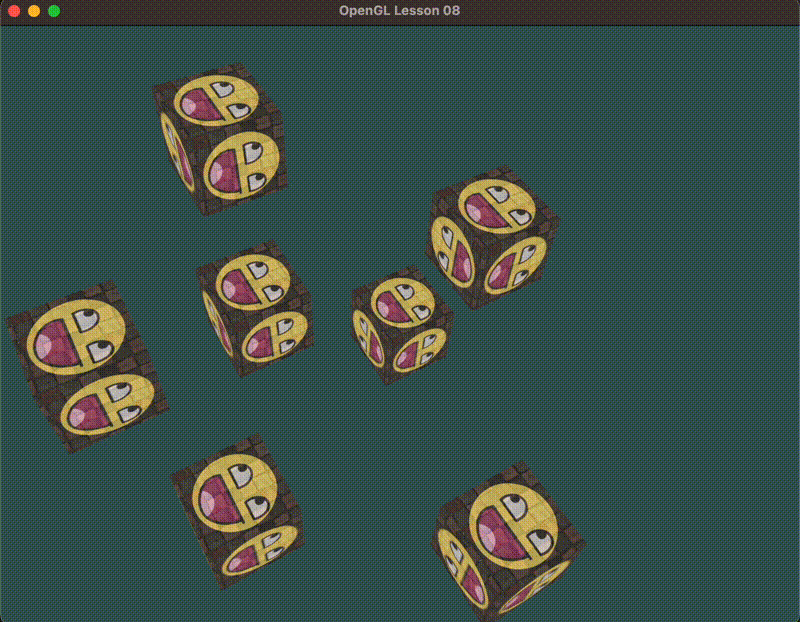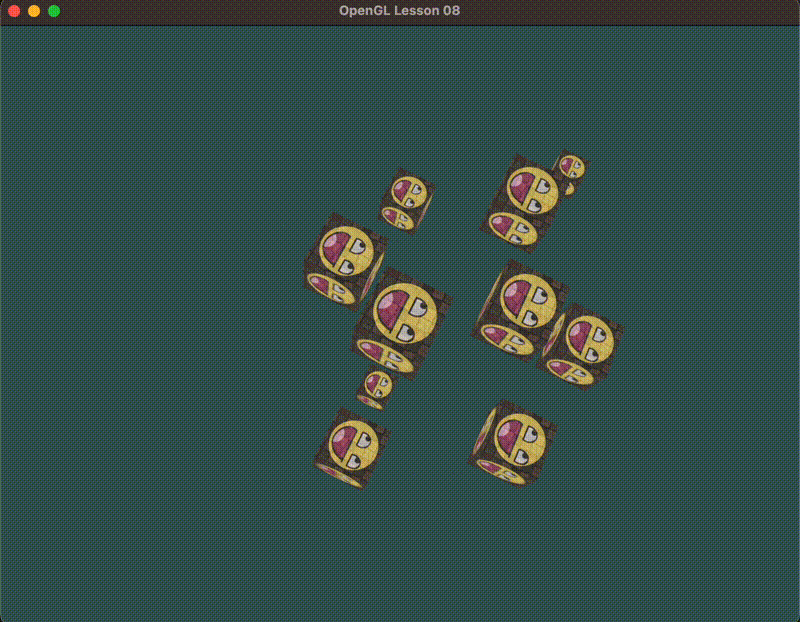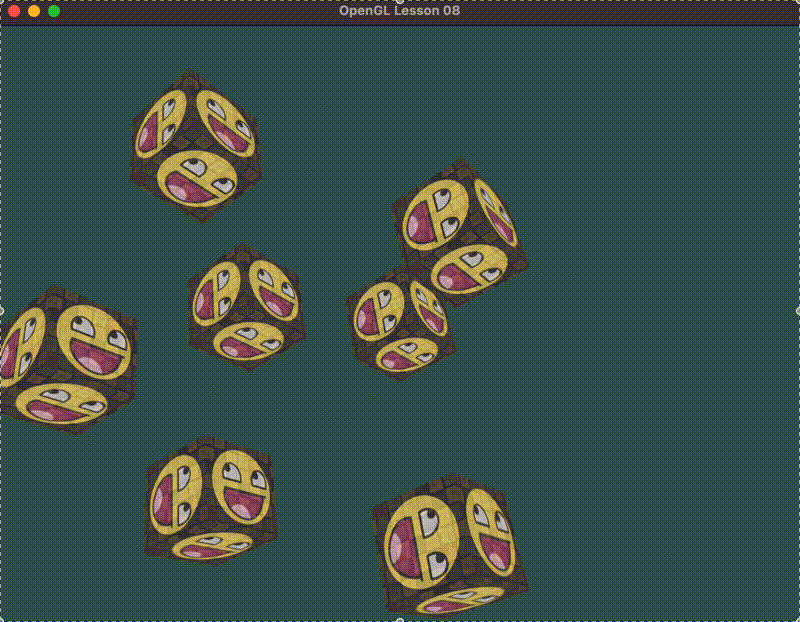
自由移动

定义相机坐标Pos， Front坐标, 世界空间的向上坐标如下:

glm::vec3 cameraPos   = glm::vec3(0.0f, 0.0f,  3.0f);
glm::vec3 cameraFront = glm::vec3(0.0f, 0.0f, -1.0f);
glm::vec3 cameraUp    = glm::vec3(0.0f, 1.0f,  0.0f);

view = glm::lookAt(cameraPos, cameraPos + cameraFront, cameraUp);

注意第二个是Front坐标，也就是相机面向的方向， 这样确保无论怎样移动，始终看向同一个方向。

键盘输入

前后移动比较简单，在z轴上加上一定的delta = cameraSpeed * cameraTarget 左右移动则要用到向量叉乘, 右手定则, 左右向量乘数对调，方向相反

static void processArrowKeys(GLFWwindow *window, glm::vec3& cameraPos, glm::vec3& cameraFront, glm::vec3& cameraUp, float deltaTime)
{
    processKeyInput(window);
    
    const float cameraSpeed = 2.5f * deltaTime; // adjust accordingly
    if (glfwGetKey(window, GLFW_KEY_W) == GLFW_PRESS or glfwGetKey(window, GLFW_KEY_UP) == GLFW_PRESS)
        cameraPos += glm::normalize(cameraFront) * cameraSpeed;
    if (glfwGetKey(window, GLFW_KEY_S) == GLFW_PRESS or glfwGetKey(window, GLFW_KEY_DOWN) == GLFW_PRESS)
        cameraPos -= glm::normalize(cameraFront) * cameraSpeed;
    if (glfwGetKey(window, GLFW_KEY_A) == GLFW_PRESS or glfwGetKey(window, GLFW_KEY_LEFT) == GLFW_PRESS)
        cameraPos -= glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
    if (glfwGetKey(window, GLFW_KEY_D) == GLFW_PRESS or glfwGetKey(window, GLFW_KEY_RIGHT) == GLFW_PRESS)
        cameraPos += glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
}

移动速度

当前使用的是常量移动速度，一个问题是，速度快的机器帧率高，即每秒render loop执行的快，视角移动也相应的快，相反慢的机器就移动就慢

为了解决这个问题，应用或游戏通常会保存一个deltatime变量，用来保存上一帧花费了多长时间。

假设一个设备，桢率=60fps, 也就是$deltatime=\frac{1}{60}$, 他就是的速度倍速就慢一些

假设一个设备，桢率=30fps, 也就是$deltatime=\frac{2}{60}$, 他就是的速度倍速就快一倍

float deltaTime = 0.0f;	// Time between current frame and last frame
float lastFrame = 0.0f; // Time of last frame
float currentFrame = glfwGetTime();
deltaTime = currentFrame - lastFrame;
lastFrame = currentFrame; 

const float cameraSpeed = 2.5f * deltaTime;

自由视角

之前相机的视角是固定的，cameraFront是一个固定值，可以通过鼠标输入改变。

欧拉角

欧拉角(Euler Angle)是可以表示3D空间中任何旋转的3个值， 一共有3种欧拉角：

欧拉角

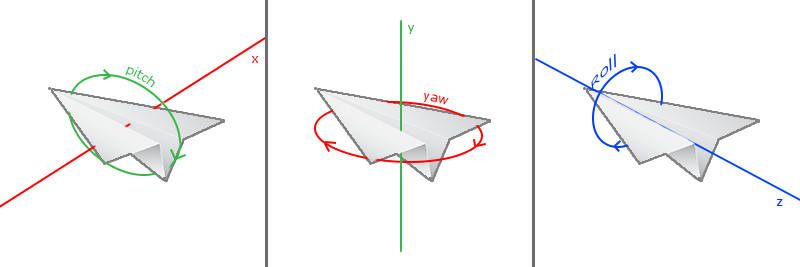
  1. 俯仰角(Pitch)是描述我们如何往上或往下看的角。
  2. 偏航角(Yaw)表示我们往左和往右看的程度。
  3. 滚转角(Roll)代表我们如何翻滚摄像机，通常在太空飞船的摄像机中使用。

每个欧拉角都有一个值来表示，把三个角结合起来我们就能够计算3D空间中任何的旋转向量了。

对于相机来说，我们只关心前两个, 假设相方向向量如下:

相机方向

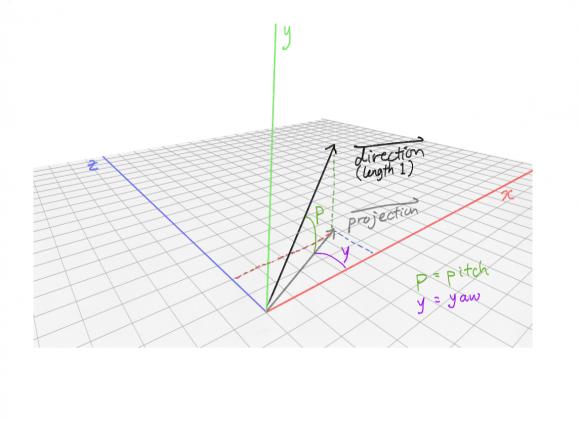
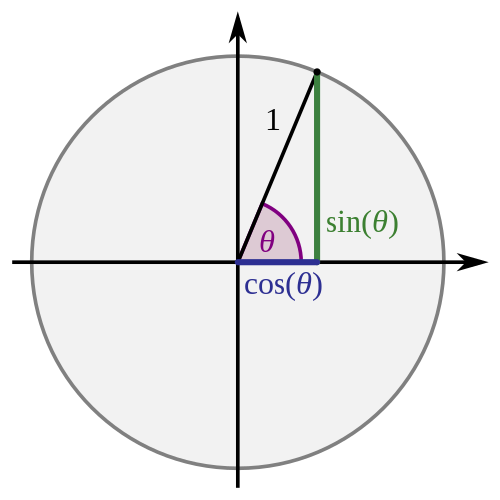
向量长度1, 俯仰角为p, 偏航角为y。

获得相机方向各个坐标轴分量，需要三角学。

$角p对边=斜边\times\sin(p)$

$角p邻边=斜边\times\cos(p)$

由于对边=1, 相机方向向量计算如下:

glm::vec3 direction;

direction.x = cos(glm::radians(yaw)) * cos(glm::radians(pitch));
direction.y = sin(glm::radians(pitch));
direction.z = sin(glm::radians(yaw)) * cos(glm::radians(pitch));

我们的相机是应该看向z轴负方向的， 但如果偏航角(Yaw)为0，相机就会看向x轴方向。

为了修正这个，yaw的初始值应该为-90;

yaw = -90.0f;

鼠标输入

俯仰角(Pitch)和偏航角(Yaw)是从鼠标(手柄或遥感)两个帧的差值获取的。水平移动决定偏航角(Yaw), 垂直移动决定俯仰角(Pitch)。

首先定义callback函数, 需要保存记录上一鼠标的值, 所以定一个struct

struct MouseCapture {
    double lastX;
    double lastY;
    double x;
    double y;
};

static MouseCapture mouseCapture;
static void mouseCaptureCallback(GLFWwindow* window, double xpos, double ypos) {
    struct MouseCapture position = {mouseCapture.x, mouseCapture.y, xpos, ypos};
    mouseCapture = position;
}

然后设置GLFW隐藏并捕光标动作。捕捉意味着光标应该停留在窗口中（除非程序失去焦点或者退出）

glfwSetInputMode(window, GLFW_CURSOR, GLFW_CURSOR_DISABLED);
glfwSetCursorPosCallback(window, mouseCaptureCallback);

相机空间

首先获得鼠标输入增量, 我们希望获的y轴·，是底部到顶部是增大的，所以鼠标捕获的值需要取负值。

然后将结果乘以敏感度(sensitivity)系数

float xoffset = capture.x - capture.lastX;
float yoffset = capture.lastY - capture.y; // reversed since y-coordinates range from bottom to top

const float sensitivity = 0.1f;
xoffset *= sensitivity;
yoffset *= sensitivity;

对于俯仰角我们要做一个限制，这样摄像机就不会发生奇怪的移动了（也会避免一些奇怪的问题）。

对于俯仰角，要让用户不能看向高于89度的地方（在90度时视角会发生逆转，所以我们把89度作为极限。

同样也不允许小于-89度。这样能够保证用户只能看到天空或脚下，但是不能超越这个限制。

if(pitch > 89.0f) pitch =  89.0f;
if(pitch < -89.0f) pitch = -89.0f;

最后将角度增量, 加到已有的变量上, 计算出cameraFront。

yaw   += xoffset;
pitch += yoffset;

glm::vec3 direction;
direction.x = cos(glm::radians(yaw)) * cos(glm::radians(pitch));
direction.y = sin(glm::radians(pitch));
direction.z = sin(glm::radians(yaw)) * cos(glm::radians(pitch));
cameraFront = glm::normalize(direction);

注意当鼠标被捕获时，第一个回调数值是鼠标进入窗口时的坐标，因为差值需要两个值相减，所以获取差值需要过滤掉第一次回调的结果。

缩放

滚轮输入

注册回调函数

glfwSetScrollCallback(window, scroll_callback); 

void scroll_callback(GLFWwindow* window, double xoffset, double yoffset)
{
    ...
}

缩放视角

限制fov在[0.0, 45.0]范围内， 当fov变小时，根据视觉投影的结果，会有画面放大的效果

  fov -= (float)yoffset;
  if (fov < 1.0f)
      fov = 1.0f;
  if (fov > 45.0f)
      fov = 45.0f;

绘制

// render loop
  glm::mat4 model = glm::mat4(1.0f);
  model = glm::translate(model, cube_positions[i]);
  model = glm::rotate(model, (float)glfwGetTime() * glm::radians(50.0f), glm::vec3(0.5f, 1.0f, 0.0f));
  glm::mat4 view = glm::lookAt(cameraPos, cameraPos + cameraFront, cameraUp);
  glm::mat4 projection = glm::perspective(glm::radians(fov), 800.0f / 600.0f, 0.1f, 100.0f);
  
  glUniformMatrix4fv(glGetUniformLocation(shaderProgram, "model"), 1, GL_FALSE, glm::value_ptr(model));
  glUniformMatrix4fv(glGetUniformLocation(shaderProgram, "view"), 1, GL_FALSE, glm::value_ptr(view));
  glUniformMatrix4fv(glGetUniformLocation(shaderProgram, "projection"), 1, GL_FALSE, glm::value_ptr(projection));

结果

源码

更多

  1. https://learnopengl.com/Getting-started/Camera
  2. https://en.wikipedia.org/wiki/Gram%E2%80%93Schmidt_process

相关推荐

上一篇 OpenGL1.7 - 空间Space

下一篇 OpenGL2.1 - 光模型Phong

评论

内容:
其他: