• 平行光
• 点光源
  • 衰减函数
  • 数值表
• 聚光
  • 手电筒
  • 模糊边缘
• 更多

学习模拟不同类型的光源，对绘制有很大帮助。

平行光

平行光(Directional Ligt), 当点光源无限远的时候，所有的光线接近于平行，光源来自同一方向。

例如太阳光，虽然不是无限远，但太阳足够远，所以我们认为太阳光就是平行光源。

因为所有的光线都是平行的，也就不在乎物体和光源的位置，计算也相对简单, 只需要光源的方向就行了lightDir

struct Light {
    vec3 direction;
  
    vec3 ambient;
    vec3 diffuse;
    vec3 specular;
};

...

void main()
{
  vec3 lightDir = normalize(-light.direction);
  ...
}

一直以来，我们使用vec3来定义光源位置或方向，有些人下换用vec4，最后一个分量w, 如果是1可以参与矩阵变换，也就是点光源。如果最后一个分量是0, 则不参与矩阵变换计算，也就是平行光源。

vec4正是旧OpenGL（固定函数式）决定光源是定向光还是位置光源(Positional Light Source)的方法，并根据它来调整光照。

点光源

平行光很适合场景的主光源，但是我们需要一些点光源(Point Light)来装饰场景。点光源是在世界中有个具体位置，它会照亮所有的方向, 光强会随着距离而衰减。可以想像下小灯泡或者火炬。

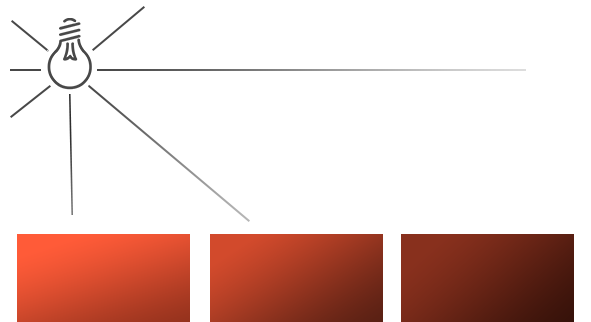
之前使用的是简单的点光源，但并没有处理强度衰减，仿佛光源特别强，衰减可以忽略不计。通常在3D场景中，我们希望点光源只照亮一个小的范围，而不是整个场景。

衰减函数

光强衰减(Attenuation)可以使用简单的线性方程$Ax + By + C = 0$, 但这种衰减看起来有点不真实。

用下面的方程，其中$K_x$为常数，d代表光源与fragment的距离:

$ F_{att} = \frac{1.0}{K_c + K_1 * d + K_q * d^2} $

1. $K_c$通常为1, 主要是为了确保分母始终大于1, 不至于是强度超过1.0
2. 一次项常数$K_1$与距离相乘，以此来按照距离线性减少光的强度。
3. 二次项常数$K_q$与距离的平方相乘，按照平方减少的特点是，距离短的时候影响不大，距离大的时候就超过一次项的影响了

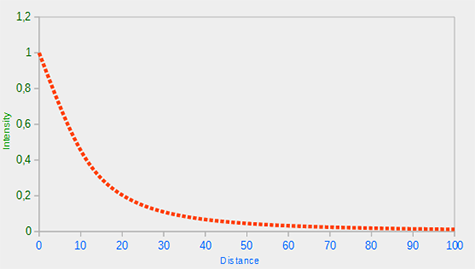
衰减曲线如上，可以看出刚开始二次项影响不大，光强度几乎线性减少。直到二次项数值超过一次项，光强会衰减的更快。

结果就是，距离光源一定范围内的时候强度很大，超出范围光强迅速减少，直到更远以更缓慢的速度减少。

数值表

新的问题是，常数设置多少？这取决于很多因数，环境，覆盖距离，光源种类等等。大多数情况下，需要调试和验证效果。

下图是模拟融合光源，覆盖范围不同情况下的数值表

Distance(d)	Constant($K_c$)		Linear($K_1$)		Quadratic($K_q$)
7	1.0	0.7	1.8
13	1.0	0.35	0.44
20	1.0	0.22	0.20
32	1.0	0.14	0.07
50	1.0	0.09	0.032
65	1.0	0.07	0.017
100	1.0	0.045	0.0075
160	1.0	0.027	0.0028
200	1.0	0.022	0.0019
325	1.0	0.014	0.0007
600	1.0	0.007	0.0002
3250	1.0	0.0014	0.000007

需要3个变量来表示光强衰减函数, 点光源仍需要知道光源的位置。

struct Light {
    vec3 position;  
  
    vec3 ambient;
    vec3 diffuse;
    vec3 specular;
 
    float constant;
    float linear;
    float quadratic;
};


float distance = length(light.position - FragPos);
float attenuation = 1.0 / (light.constant + light.linear * distance + light.quadratic * (distance * distance));    

使用点光源覆盖距离为50, 设置对应数值查表如下:

glUniform1f(glGetUniformLocation(shaderProgram, "light.constant"),  1.0f);
glUniform1f(glGetUniformLocation(shaderProgram, "light.linear"),    0.09f);
glUniform1f(glGetUniformLocation(shaderProgram, "light.quadratic"), 0.032f);

最后把光强，设置给Phong模型的各个分量

ambient  *= attenuation; 
diffuse  *= attenuation;
specular *= attenuation; 

代码

聚光

聚光(spotlight), 聚光不像点光源照亮所有方向，聚光在3D环境中有特定的发射方向。结果就是聚光下有颜色，其他部分都是黑的。

所以OpenGL中，聚光需要光源位置，方向，还有切光角(Cutoff Angle)，切光角用来设置聚光照亮范围的的半径。

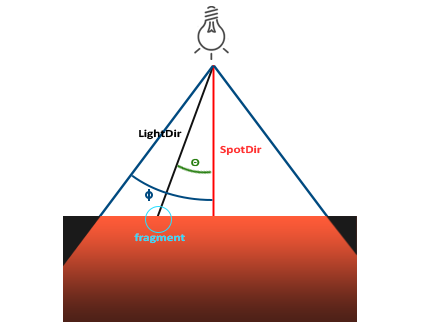
1. $\vec{LightDir}$从Fragment指向光源的向量
2. $\vec{SpotDir}$是聚光照亮的方向
3. $\phi$是切光角，用来制定聚光的半径，半径之外是漆黑的。
4. $\theta$是$\vec{LightDir}$与$\vec{SpotDir}$的夹角，如果在聚光灯之内其值应该小于切光角

通过$-\vec{LightDir}$与$\vec{SpotDir}$的点乘，获得$\theta$的$\cos$值，然后将将其与切光角$\cos$值比较

手电筒

手电筒是一种聚光，通常手电筒在观察者的位置并且从观察着的视角直接指向物体, 与普通聚光不同的是手电筒会随着人物移动, 如下宝图:

定义光源如下, 其中角度使用$\cos$值，原因是在Fragment Shader中会用到向量点乘，返回的就是$\cos$值, 如果每次都转换角度再比较，结果重复还耗费资源。注意$\cos$角度越大值越小

struct Light {
    vec3 position;
    vec3 direction;
    float cutOff;
    
    vec3 ambient;
    vec3 diffuse;
    vec3 specular;
};

...
float theta = dot(lightDir, normalize(-light.direction));
if(theta > light.cutOff) {       
  // do lighting calculations
} else {  
  // use ambient light so scene isn't completely dark outside the spotlight.
  color = vec4(light.ambient * vec3(texture(material.diffuse, TexCoords)), 1.0);
}

设置参数

glUniform3f(glGetUniformLocation(shaderProgram, "light.position"), cameraPos.x, cameraPos.y, cameraPos.z);
glUniform3f(glGetUniformLocation(shaderProgram, "light.direction"), cameraFront.x, cameraFront.y, cameraFront.z);
glUniform1f(glGetUniformLocation(shaderProgram, "light.cutOff"), glm::cos(glm::radians(12.5f)));

模糊边缘

上面看起来有点假，主要是聚光边缘明暗变化太明显。为了平滑软化边缘需要模拟聚光的内圆锥(Inner Cone)和外圆锥(Outer Cone)

内圆锥我们用上面的就行，但还需要一个光线渐弱的外圆锥。

我们需要一个角度更大的切光角(其结果是$\cos$更小的值)。如果在内外圆锥之间，需要计算渐变，其强度如下公式

$ I = \frac{\Theta - \gamma}{\epsilon} $

1. $\theta$是$\vec{LightDir}$与$\vec{SpotDir}$的夹角, 即照亮Fragment的光线与光源照射方向的夹角
2. $\gamma$(gamma)外圆锥的$\cos$值
3. $\epsilon$(epsilon)是内圆锥$\phi$(phi)与外圆锥$\gamma$(gamma)的$\cos$差值

$\theta$	$\theta$(度)	$\phi$(内圆锥)	$\phi$(度)	$\gamma$(外圆锥)	$\gamma$(度)	$\epsilon$	I
0.87	30	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.87 - 0.82 / 0.09 = 0.56
0.9	26	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.9 - 0.82 / 0.09 = 0.89
0.97	14	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.97 - 0.82 / 0.09 = 1.67
0.83	34	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.83 - 0.82 / 0.09 = 0.11
0.64	50	0.91	25	0.82	35	0.91 - 0.82 = 0.09	0.64 - 0.82 / 0.09 = -2.0
0.966	15	0.9978	12.5	0.953	17.5	0.9978 - 0.953 = 0.0448	0.966 - 0.953 / 0.0448 = 0.29

从上表看出， 计算时有超出[0.0, 1.0]区间的，在内圆锥范围内结果>1, 两个光锥之间的在[0, 1], 超出外圆锥的<1。

如果使用clamp函数，把数值压缩到[0, 1]范围内，就不需要if-else判断了。

float theta     = dot(lightDir, normalize(-light.direction));
float epsilon   = light.cutOff - light.outerCutOff;
float intensity = clamp((theta - light.outerCutOff) / epsilon, 0.0, 1.0);    
...
// we'll leave ambient unaffected so we always have a little light.
diffuse  *= intensity;
specular *= intensity;
...

最后设置外圆锥

glUniform1f(glGetUniformLocation(shaderProgram, "light.outerCutOff"), glm::cos(glm::radians(17.5f)));

代码

更多

1. https://learnopengl.com/Lighting/Light-casters