向量
向量拥有数值和方向, 数学表示如下:
$ \vec{v} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} $
向量与标量运算
向量与标量加法如下:
$ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + x \rightarrow \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + \begin{pmatrix} x \\ x \\ x \end{pmatrix} = \begin{pmatrix} 1 + x \\ 2 + x \\ 3 + x \end{pmatrix} $
上面的+可以换成减号-, 乘号*, 除号÷
向量取反
向量取反后，方向相反，相当于-1数乘向量
$ -\vec{v} = -\begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} -x \\ -y \\ -z \end{pmatrix} $
向量加法
几何
三角形或平行四边形法则
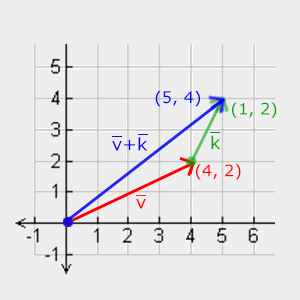
数学
$ \vec{v} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, \vec{k} = \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix} \rightarrow \vec{v} + \vec{k} = \begin{pmatrix} 1 + 4 \\ 2 + 5 \\ 3 + 6 \end{pmatrix} = \begin{pmatrix} 5 \\ 7 \\ 9 \end{pmatrix} $
向量减法
几何
$\vec{w} - \vec{v}$可以理解为以$\vec{v}$的终点为始点，以$\vec{w}$的终点为终点的向量
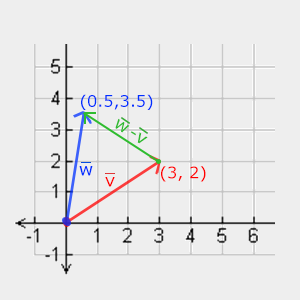
数学
$ \vec{v} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, \vec{k} = \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix} \rightarrow \vec{v} + -\vec{k} = \begin{pmatrix} 1 + (-4) \\ 2 + (-5) \\ 3 + (-6) \end{pmatrix} = \begin{pmatrix} -3 \\ -3 \\ -3 \end{pmatrix} $
向量长度
将向量起点平移到坐标原点，终点到原点的距离 $ ｜\vec{v}｜ = \sqrt{x^2 + y^2} $
单位向量
长度为1的向量
$ n\hat{} = \frac{\vec{v}}{｜\vec{v}｜} $
向量内积(点乘)
几何
点乘的结果表示$\vec{v}$在$\vec{k}$方向上的投影与$｜\vec{k}｜$的乘积
- $\vec{v}\cdot\vec{k} > 0$则方向基本相同，夹角在0°到90°之间
- $\vec{v}\cdot\vec{k} = 0$则正交，相互垂直
- $\vec{v}\cdot\vec{k} < 0$则方向基本相反，夹角在90°到180°之间
$ \vec{v}\cdot\vec{k} = ｜\vec{v}｜ * ｜\vec{k}｜ * \cos\theta $
数学
$ \begin{pmatrix} A_1 \\ A_2 \\ A_3 \end{pmatrix} \cdot \begin{pmatrix} B_1 \\ B_2 \\ B_3 \end{pmatrix} = (A_1 * B_1) + (A_2 * B_2) + (A_3 * B_3) = -0.8 $
向量外积(叉乘)
外积是3D空间中的定义，两个不平行的向量，可以确定一个平面，外积的方向垂直于这个平面，通过右手法则确定。 如果输入的两个向量也是正交的，那么叉乘之后将会产生3个互相正交的向量
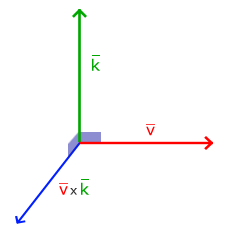
几何
如果以向量$\vec{a}$与$\vec{b}$为边构成一个平行四边形，那么这两个向量外积的模长与这个平行四边形的面积相等。
$\vec{a}\times\vec{b} = ｜\vec{b}｜ * ｜\vec{b}｜ * \sin\theta\vec{n}$
数学
$ \begin{pmatrix} A_1 \\ A_2 \\ A_3 \end{pmatrix} \times \begin{pmatrix} B_1 \\ B_2 \\ B_3 \end{pmatrix} = \begin{pmatrix} A_2\cdot{B_3} - A_3\cdot{B_2} \\ A_3\cdot{B_1} - A_1\cdot{B_3} \\ A_1\cdot{B_2} - A_2\cdot{B_1} \end{pmatrix} $
矩阵
$ \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} $
矩阵加法
同型矩阵可以相加，每一项分别加起来
$ \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} + \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix} = \begin{pmatrix} 1 + 5 & 2 + 6 \\ 3 + 7 & 4 + 8 \end{pmatrix} = \begin{pmatrix} 6 & 8 \\ 10 & 12 \end{pmatrix} $
矩阵减法
同型矩阵可以相加，第一个矩阵每一项减去第二个矩阵的对应项
$ \begin{pmatrix} 4 & 2 \\ 1 & 6 \end{pmatrix} - \begin{pmatrix} 2 & 4 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 - 2 & 2 - 4 \\ 1 - 0 & 6 -1 \end{pmatrix} = \begin{pmatrix} 2 & -2 \\ 1 & 5 \end{pmatrix} $
矩阵数乘
数字乘以矩阵的每一项
$ 2 \cdot \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} = \begin{pmatrix} 2 * 1 & 2 * 2 \\ 2 * 3 & 2 * 4 \end{pmatrix} = \begin{pmatrix} 2 & 4 \\ 6 & 8 \end{pmatrix} $
矩阵乘法
相乘交换不相等
$A\cdot{B}\neq{B}\cdot{A}$
$C_{ij}$等于矩阵A的第i行乘以B的第j列，结果相加:
$ \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix} = \begin{pmatrix} 1 * 5 + 2 * 7 & 1 * 6 + 2 * 8 \\ 3 * 5 + 4 * 7 & 3 * 6 + 4 * 8 \end{pmatrix} = \begin{pmatrix} 19 & 22 \\ 43 & 50 \end{pmatrix} $
两个矩阵相乘，必须左边的列数 = 右边的行数.
$A_{mk} * B_{kn} = C_{mn}$
Transform
到目前为止，向量可以表示坐标，颜色，纹理坐标。
N维向量是特殊的$N\times1$矩阵
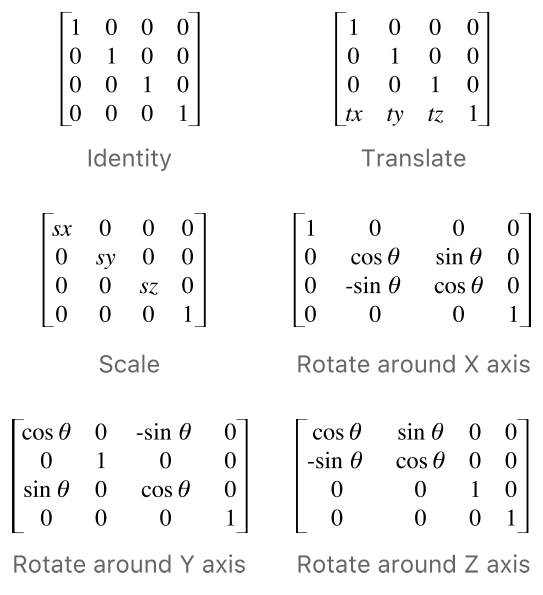
Identity
OpenGL通常使用$4\times{4}$矩阵, 单位矩阵只有主对角线(左上到右下)是1，其他都是0, 单位矩阵与向量相乘，向量保持不变
$ \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} = \begin{pmatrix} 1 * 1 \\ 1 * 2 \\ 1 * 3 \\ 1 * 4 \end{pmatrix} \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} $
Scaling
对向量缩放(Scaling)是改变向量的长度，但是方向不变
OpenGL通常进行2D/3D操作，可以定义3个缩放变量, 每个变量缩放一个轴(x, y或z)
以向量$\vec{v} = \begin{pmatrix} 3 \\ 2 \end{pmatrix}$ 为例， 把宽度缩小至1/2，把长度放大至2倍。
得到向量$\vec{s} = \begin{pmatrix} 1.5 \\ 4 \end{pmatrix}$
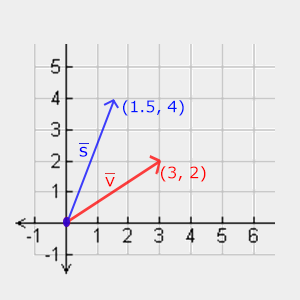
OpenGL通常对3D进行操作，对于2D可以设置z轴的缩放系数=1，这样z轴就不会改变了， 刚刚做的事不均匀(Non-uniform)缩放。如果每个轴缩放因子(Scaling Factor)都一样, 成为均匀缩放(Uniform Scale)
在单位矩阵基础上构造scaling矩阵
$ \begin{pmatrix} S_1 & 0 & 0 & 0 \\ 0 & S_2 & 0 & 0 \\ 0 & 0 & S_3 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} S_1 * x \\ S_2 * y \\ S_3 * z \\ 1 \end{pmatrix} $
Translation
位移(Translation)是在原来向量的基础上加上另一个向量，从而获得一个新的不同位置的向量, 可以回想下向量的三角形法则
构造translation矩阵，有了位移矩阵，就可以在(x, y, z)三个方向上移动物体:
$ \begin{pmatrix} 1 & 0 & 0 & T_x \\ 0 & 1 & 0 & T_y \\ 0 & 0 & 1 & T_z \\ 0 & 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x + T_x \\ y + T_y \\ z + T_z \\ 1 \end{pmatrix} $
向量的w分量也叫齐次坐标，想要从齐次向量得到3D向量，我们可以把x、y和z坐标分别除以w坐标。我们通常不会注意这个问题，因为w分量通常是1.0。使用齐次坐标有几点好处：它允许我们在3D向量上进行位移，因为3为坐标没办法和4x4矩阵想成。再有就是w值创建3D观察视角。 如果$w=0$, 这个坐标就是方向向量，不能移动
Rotation
旋转(Rotation)在2D或3D空间中用角(Angle)来表示
$ 角度 = 弧度 * (180.0f / PI) 弧度 = 角度 * (PI / 180.0f) $
$\vec{v}$由$\vec{k}$顺时针旋转72度所得:
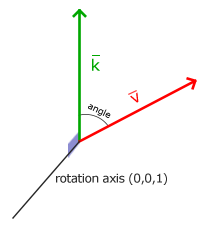
3D空间旋转需要指定角度(angle)和旋转轴(rotation axis), 物体会沿着给定的旋转轴旋转特定角度, 当2D向量在3D空间中旋转时，我们把旋转轴设为z轴。
使用三角学，给定一个角度，可以把一个向量变换为一个经过旋转的新向量。这通常是使用一系列正弦和余弦函数（一般简称sin和cos）各种巧妙的组合得到的。
旋转矩阵在3D空间中每个单位轴都有不同定义，旋转角度用$\theta$表示：
X轴 $ \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta & 0 \\ 0 & \sin\theta & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x \\ \cos\theta * y - \sin\theta * z \\ \sin\theta * y + \cos\theta * z \\ 1 \end{pmatrix} $
y轴
$ \begin{pmatrix} \cos\theta & 0 & \sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\theta & 0 & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \cos\theta * x + \sin\theta * z \\ y \\ -\sin\theta * x + \cos\theta * z \\ 1 \end{pmatrix} $
z轴
$ \begin{pmatrix} \cos\theta & -\sin\theta & 0 & 0 \\ \sin\theta & \cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \cos\theta * x - \sin\theta * y \\ \sin\theta * x - \cos\theta * y \\ z \\ 1 \end{pmatrix} $
万向节锁
万向节锁是3D空间中，一个轴的自由度消失的问题，万向节锁发生在当两个轴处于同一平面时，将旋转锁死在一个2D空间中。
例如当绿色环和粉色环在同一个平面时:
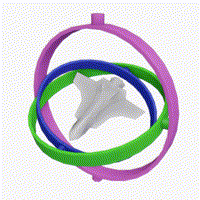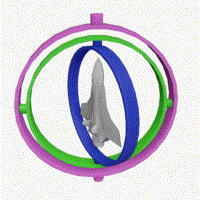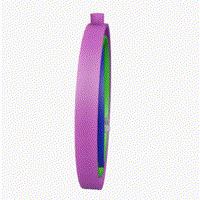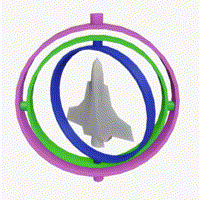
利用旋转矩阵我们可以把任意位置向量沿一个单位旋转轴进行旋转。也可以将多个矩阵复合，比如先沿着x轴旋转再沿着y轴旋转。但是这会很快导致一个问题——万向节锁（Gimbal Lock)
一个更好的解决方案是，沿着任意轴 $R=(R_x, R_y, R_z)$ 旋转，而且这样的矩阵是存在的
$ \begin{bmatrix} \cos \theta + \color{red}{R_x}^2(1 - \cos \theta) & \color{red}{R_x}\color{green}{R_y}(1 - \cos \theta) - \color{blue}{R_z} \sin \theta & \color{red}{R_x}\color{blue}{R_z}(1 - \cos \theta) + \color{green}{R_y} \sin \theta & 0 \\ \color{green}{R_y}\color{red}{R_x} (1 - \cos \theta) + \color{blue}{R_z} \sin \theta & \cos \theta + \color{green}{R_y}^2(1 - \cos \theta) & \color{green}{R_y}\color{blue}{R_z}(1 - \cos \theta) - \color{red}{R_x} \sin \theta & 0 \\ \color{blue}{R_z}\color{red}{R_x}(1 - \cos \theta) - \color{green}{R_y} \sin \theta & \color{blue}{R_z}\color{green}{R_y}(1 - \cos \theta) + \color{red}{R_x} \sin \theta & \cos \theta + \color{blue}{R_z}^2(1 - \cos \theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} $
但即使这样一个矩阵也不能完全解决万向节死锁问题（尽管会极大地避免）。避免万向死锁的真正解决方案是使用四元数(Quaternion)，它不仅更安全，而且计算会更有效率
Combine
一下结果基于矩阵乘以向量.
使用矩阵的好处是，根据矩阵乘法，我们可以将多个变换(transformations)合并(combine)到一个矩阵结果中
假设我们有一个顶点(x, y, z)，我们希望将其缩放2倍，然后位移(1, 2, 3)个单位。我们需要一个位移和缩放矩阵来完成这些变换。结果的变换矩阵看起来像这样：
$ Trans . Scale = \begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} . \begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} = \begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} $
注意，当矩阵相乘时我们先写位移再写缩放变换的。矩阵乘法是不遵守交换律的，这意味着它们的顺序很重要。当矩阵相乘时，在最右边的矩阵是第一个与向量相乘的，所以你应该从右向左读这个乘法。建议您在组合矩阵时，先进行缩放操作，然后是旋转，最后才是位移，否则它们会（消极地）互相影响。比如，如果你先位移再缩放，位移的向量也会同样被缩放（比如向某方向移动2米，2米也许会被缩放成1米）！
用最终的变换矩阵左乘我们的向量会得到以下结果：
$ \begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} . \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \color{red}2x + \color{red}1 \\ \color{green}2y + \color{green}2 \\ \color{blue}2z + \color{blue}3 \\ 1 \end{bmatrix} $
如果基于向量乘以矩阵, 那么建议的组合顺序应该相反。
GLSL
Vertex Shader
定义mat4变量，支持上述Transform操作
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aColor;
out vec3 ourColor;
uniform mat4 transform;
void main()
{
gl_Position = transform * vec4(aPos, 1.0f);
ourColor = aColor;
}
Fragment Shader
#version 330 core
out vec4 FragColor;
in vec3 ourColor;
void main()
{
FragColor = vec4(ourColor, 1.0);
}
绘制
使用现成的GLM库
转换(Transform)矩阵, 先放大2，再z轴旋转，旋转轴要确保是个单位向量
#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>
// render loop
glUseProgram(shaderProgram);
glm::mat4 trans = glm::mat4(1.0f);
trans = glm::rotate(trans, (float)glfwGetTime(), glm::vec3(0.0f, 0.0f, 1.0f));
trans = glm::scale(trans, glm::vec3(2, 2, 2));
unsigned int transformLoc = glGetUniformLocation(shaderProgram, "transform");
glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));
